La grande famille des modèles de Machine Learning supervisé

Temps de lecture estimé : 10 minutes

Intelligence Artificielle, Machine Learning, Deep Learning… Des buzz words ou des domaines d’avenir? Avant de répondre à cette question, il convient de donner une vision plus claire des modèles statistiques qui se cachent derrière ces mots. Rassurez-vous, je ne vais pas vous infliger des formules mathématiques difficiles à digérer. Cet article, propose plutôt une découverte à large spectre des principales familles de modèles et des intuitions qu’il y a derrière sans rentrer dans leurs preuves mathématiques.

Naissance de l’Intelligence Artificielle

L’idée que les machines peuvent acquérir une intelligence par le calcul est apparue dans les années 50. D’abord, Alan Turing qui publie son fameux “Test de Turing” pour décider si une machine est intelligente ou pas. Ensuite en 1956, les principaux chercheurs qui vont faire naitre l’Intelligence Artificielle se réunissent pour une conférence scientifique au Dartmouth College. A partir de cette date, les premiers modèles statistiques permettant d’apprendre à classer des objets ont commencé à apparaitre, c’est la naissance du Machine Learning. Plusieurs types de modèles ont été proposés: des modèles linéaires, des modèles probabilistes, des arbres de décision, des réseaux de neurones, etc. Plus récemment, les capacités de calculs accrues des machines, notamment avec des GPUs toujours plus puissants, permettent d’empiler de plus en plus de couches dans les réseaux de neurones, c’est la naissance du Deep Learning. Mais avant de parler de couches et de réseaux de neurones, commençons par faire une distinction basique.

Le supervisé et le non supervisé

Avant de présenter l’intuition derrière les principaux modèles de Machine Learning, je souhaite distinguer deux approches : (i) on parle d’apprentissage supervisé lorsque les données d’entrées sont étiquetées (ou labellisées) et (ii) d’apprentissage non supervisé lorsque les données d’entrées ne sont pas étiquetées. Prenons deux exemples pour illustrer cette différence:

Cas numéro 1 : Je possède 10 000 emails où chaque email est labellisé manuellement soit par la mention SPAM soit par la mention NON SPAM. Mes données sont déjà étiquetées, je suis donc dans un cas supervisé. Je peux apprendre un modèle statistique sur ces données qui pourra être utilisé sur de nouveaux emails pour décider s’il s’agit de SPAM ou NON.

Cas numéro 2 : Je possède 10 000 articles de news qui ne sont pas associés à des catégories. Ces articles peuvent aborder des sujets différents (sport, politique, tech, etc.) que je ne connais pas à l’avance. Mes données ne sont pas étiquetées, je suis donc dans un cas non supervisé. Je peux apprendre un modèle qui va essayer de regrouper les articles qui se ressemblent (ou qui parle des mêmes thématiques).

Pour simplifier, on peut donc dire que lorsqu’on fait de l’apprentissage supervisé on connait exactement les catégories qu’on cherche, alors que dans l’apprentissage non supervisé on ne connait pas à l’avance les catégories recherchées.

Une autre façon de faire de l’apprentissage automatique peut parfois être distinguée : il s’agit du reinforcement learning qui permet à un agent d’apprendre en interagissant avec son environnement. Dans cet article, je vais me concentrer uniquement sur les modèles de Machine Learning supervisé. Nous allons partir des modèles les plus simples et monter en complexité au fur et à mesure. Il faut dire qu’à performance égale, un modèle simple sera souvent privilégié car les modèles complexes auront tendance à sur-apprendre.

Les modèles linéaires

Supposons que l’on souhaite prédire le loyer d’un appartement à partir de sa surface. Le premier modèle auquel on peut penser est un modèle linéaire de la forme : Loyer = a * Surface + b. Apprendre ce modèle consiste à trouver les valeurs des paramètres a et b. Cela suppose bien évidemment une relation linéaire entre la variable à prédire (dans notre exemple le loyer) et la (ou les) variable(s) qui décrivent nos données (dans notre exemple la surface). Ce modèle est donc bien adapté si les données d’apprentissage ressemblent à la figure ci-dessous (ce qui n’est pas toujours le cas) :

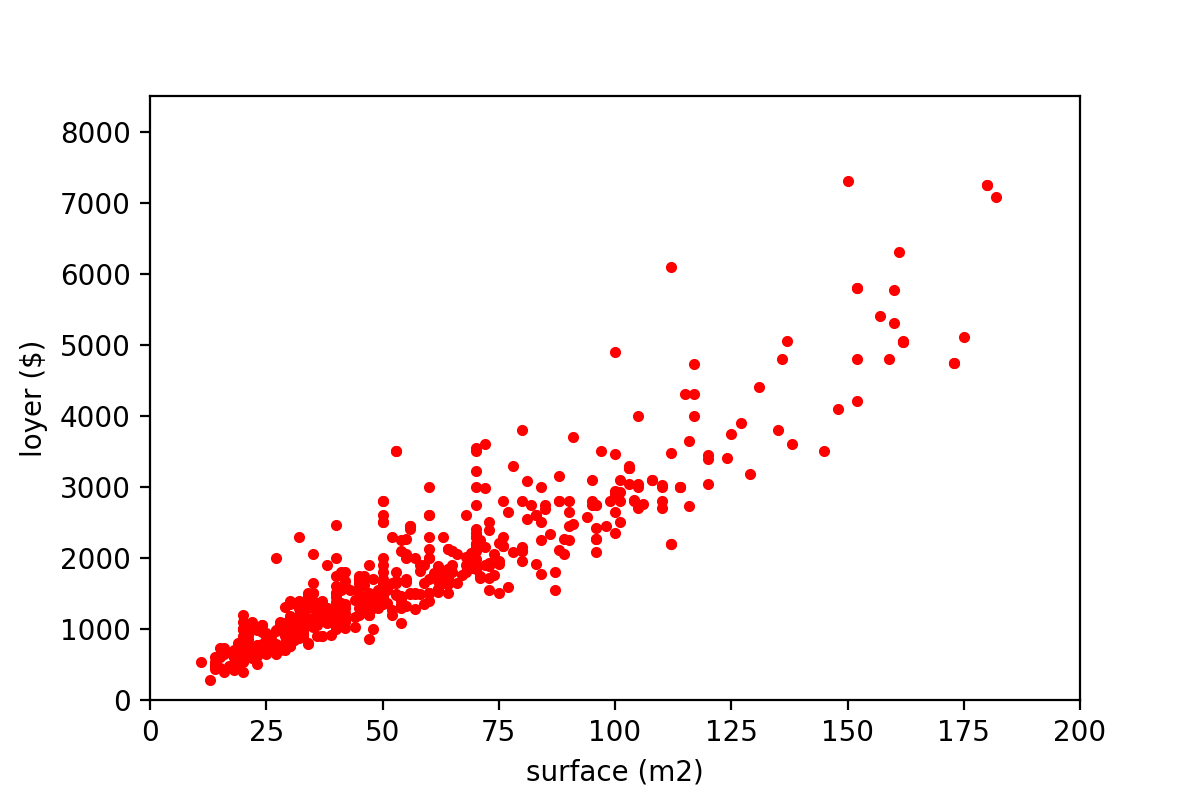
De plus le modèle présenté ci-dessus permet de prédire une variable numérique (comme le loyer). Pour prédire une variable catégorielle (e.g. : SPAM vs. NON SPAM), on utilise en général une fonction logistique qui permet de convertir n’importe quelle valeur réelle en une valeur comprise entre 0 et 1. Par exemple dans le cas de la classification d’emails, cette valeur correspond à une probabilité que l’email soit un SPAM. Si cette probabilité se rapproche de 1 on prédit que l’email est un spam, si elle se rapproche de 0 on prédit qu’il s’agit d’un non spam. La figure ci-dessous présente la courbe d’une fonction logistique souvent utilisée en Machine Learning appelée Sigmoïde.

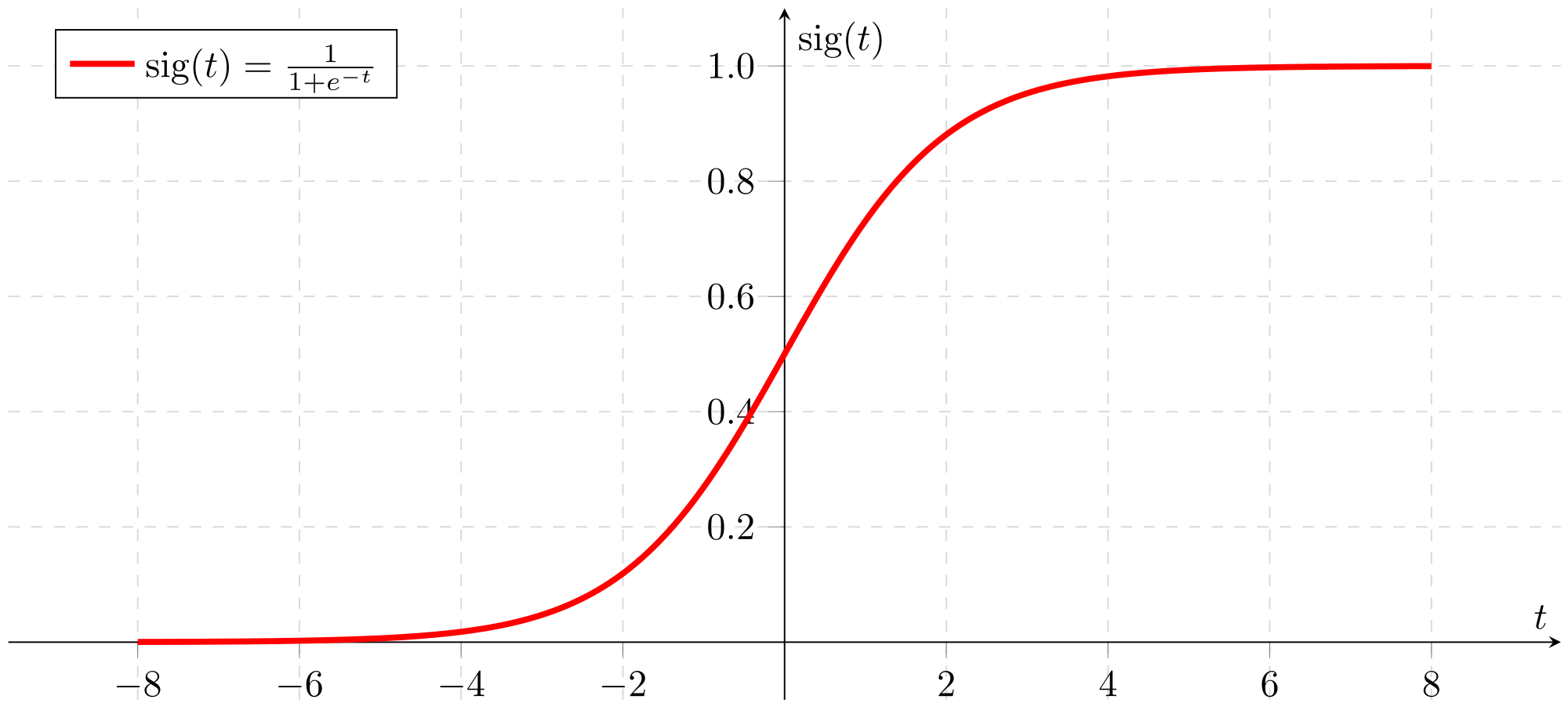
Les arbres de décision

Comme leur nom l’indique, les arbres de décision permettent de classer des objets en effectuant des décisions successives sur la base de leurs variables. Les noeuds de l’arbre représentent ces décisions alors que les feuilles représentent les valeurs de la variable cible (à prédire). La figure ci-dessous présente un exemple d’arbre de décision permettant de prédire si une personne possède ou pas un ordinateur.

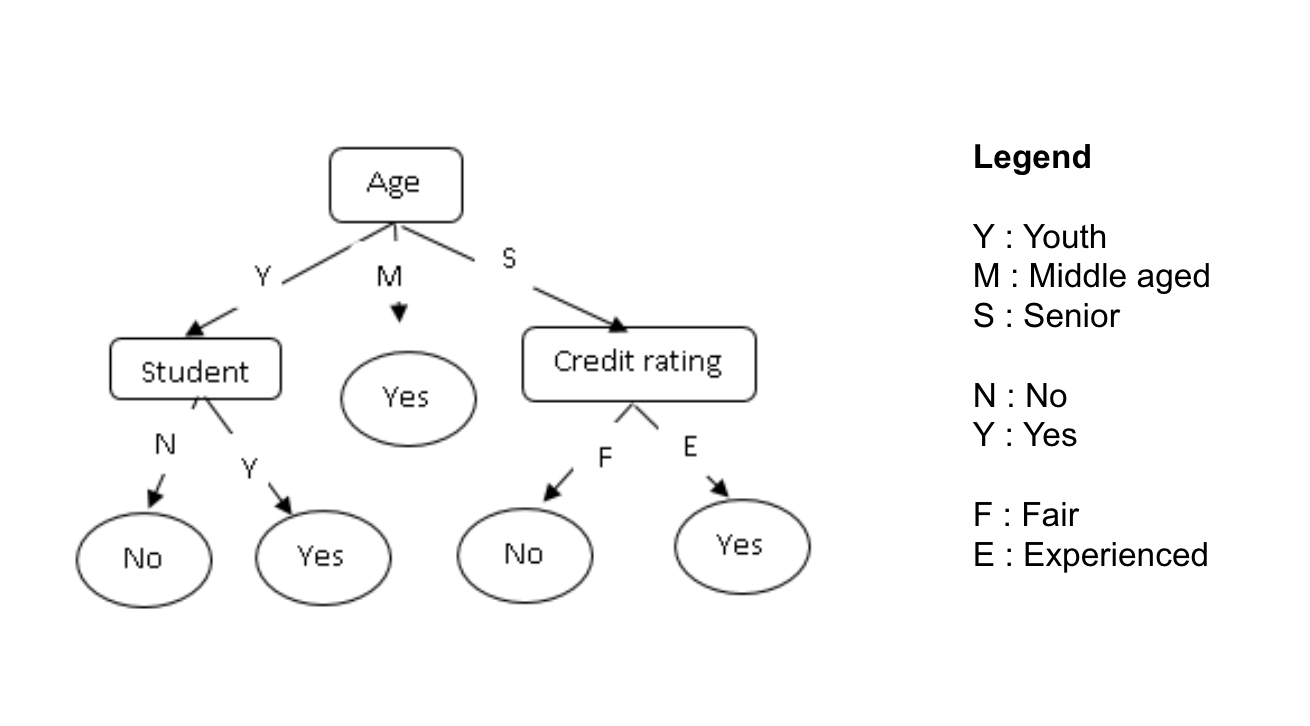
Comme tout algorithme supervisé, on utilise des données d’apprentissage pour lesquelles la valeur de la variable cible est connue afin de construire notre arbre de décision. Tout l’enjeu de l’apprentissage est de choisir à chaque étape la (ou les) variable(s) à utiliser sur un noeud donné. Plusieurs algorithmes existent permettant de générer des arbres de décision (ID3, C4.5, CART, etc.). Chaque algorithme utilise un critère pour choisir la variable à utiliser sur un noeud (gain d’information, entropie, etc.). Je vais vous épargner leurs formules un peu barbares mais vous pouvez retenir qu’on choisit la variable d’entrée (par exemple l’âge) ayant le plus d’impact sur la variable cible à prédire (possède ou pas un ordinateur).

Plusieurs hyper-paramètres peuvent être ajustés par les Data Scientists lors de l’apprentissage des arbres de décision comme: le critère de segmentation (gain d’information, entropie, etc.), la profondeur maximale de l’arbre, le nombre minimum d’objets pour faire un noeud de segmentation, etc. Ces hyper-paramètres sont le plus souvent choisis en testant le maximum de valeurs possibles en validation croisée.

Les SVMs (Support Vector Machines)

Les machines à vecteurs de support sont le plus souvent utilisées sur des données avec beaucoup de variables. L’idée des SVMs est de chercher un hyperplan (un séparateur linéaire) qui sépare au mieux les objets de chaque catégorie. En effet, il peut y avoir une infinité de séparateurs possibles comme le montre la figure ci-dessous. Le meilleur hyperplan selon les SVMs est celui qui maximise les marges avec les objets de chaque catégorie. Ces objets sont d’ailleurs appelés “vecteurs de support” car ils supportent les hyper-plans parallèles (voir la figure ci-dessous).

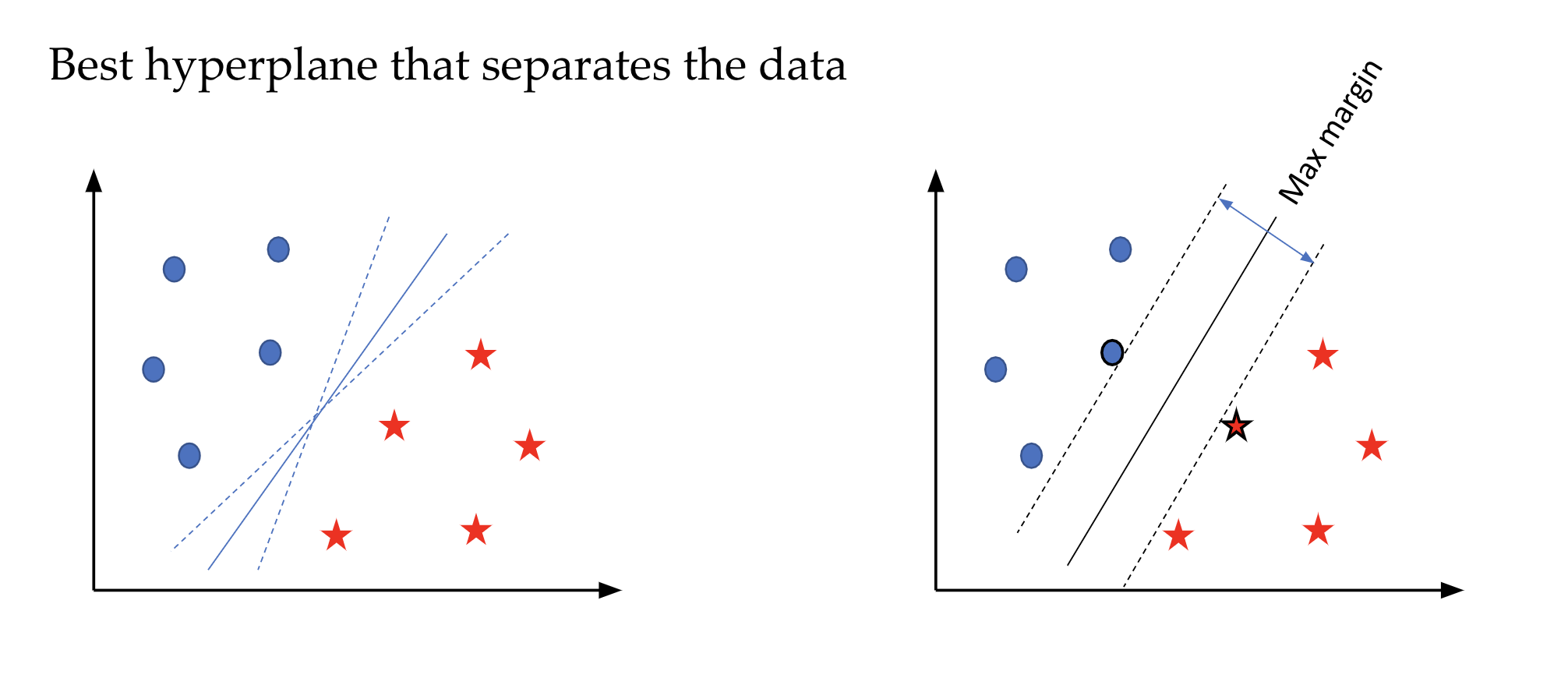
On parle de façon générale d’hyperplan mais la nature du séparateur linéaire dépend du nombre de variables ou d’attributs. Sur la figure ci-dessus, nous avons deux variables quantitatives représentées sur les deux axes orthogonaux, le séparateur est donc une droite.

Par contre, il est fréquent qu’il n’y ait pas d’hyperplan capable de séparer parfaitement les données. Dans ce cas, on peut permettre qu’il y ait un certain nombre d’erreurs. L’optimisation de l’hyper-paramètre C permet justement de fixer un compromis entre la maximisation des marges et la minimisation des erreurs.

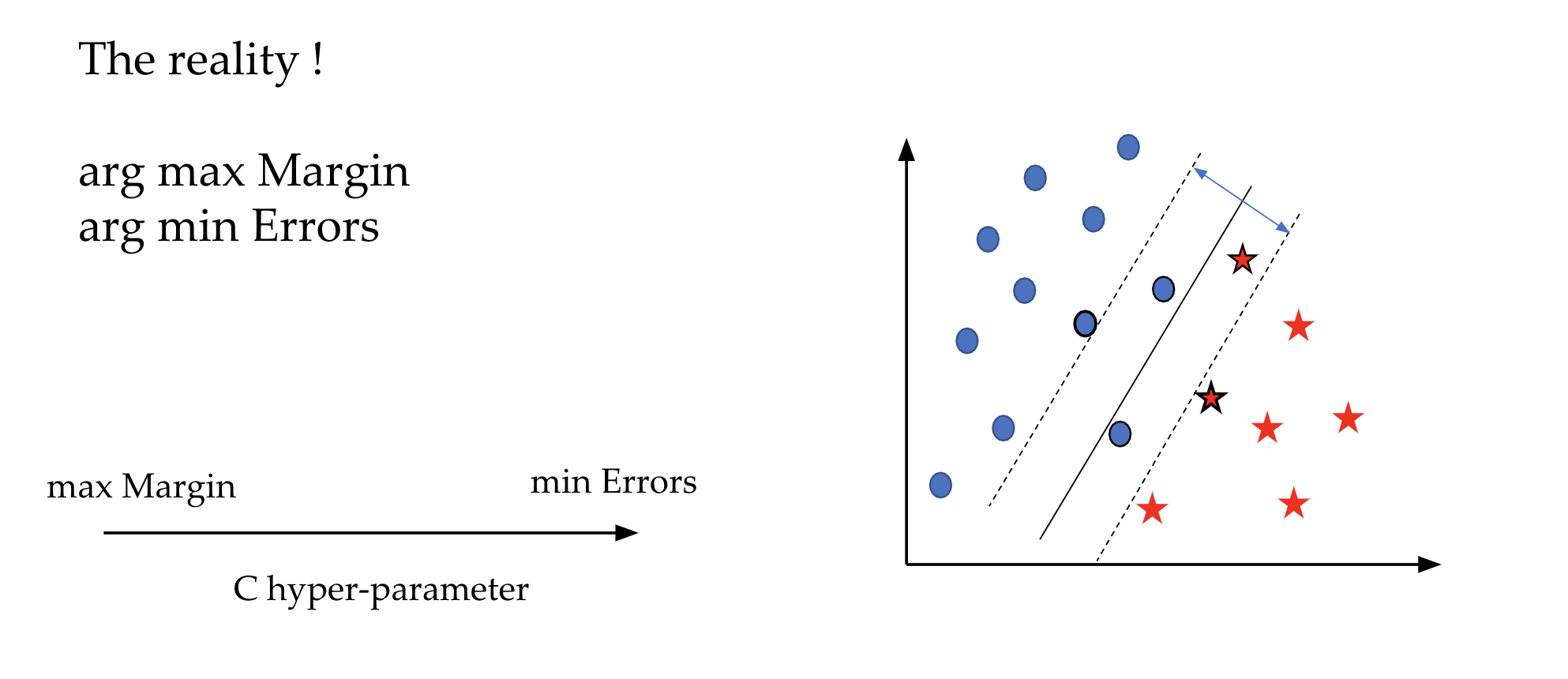
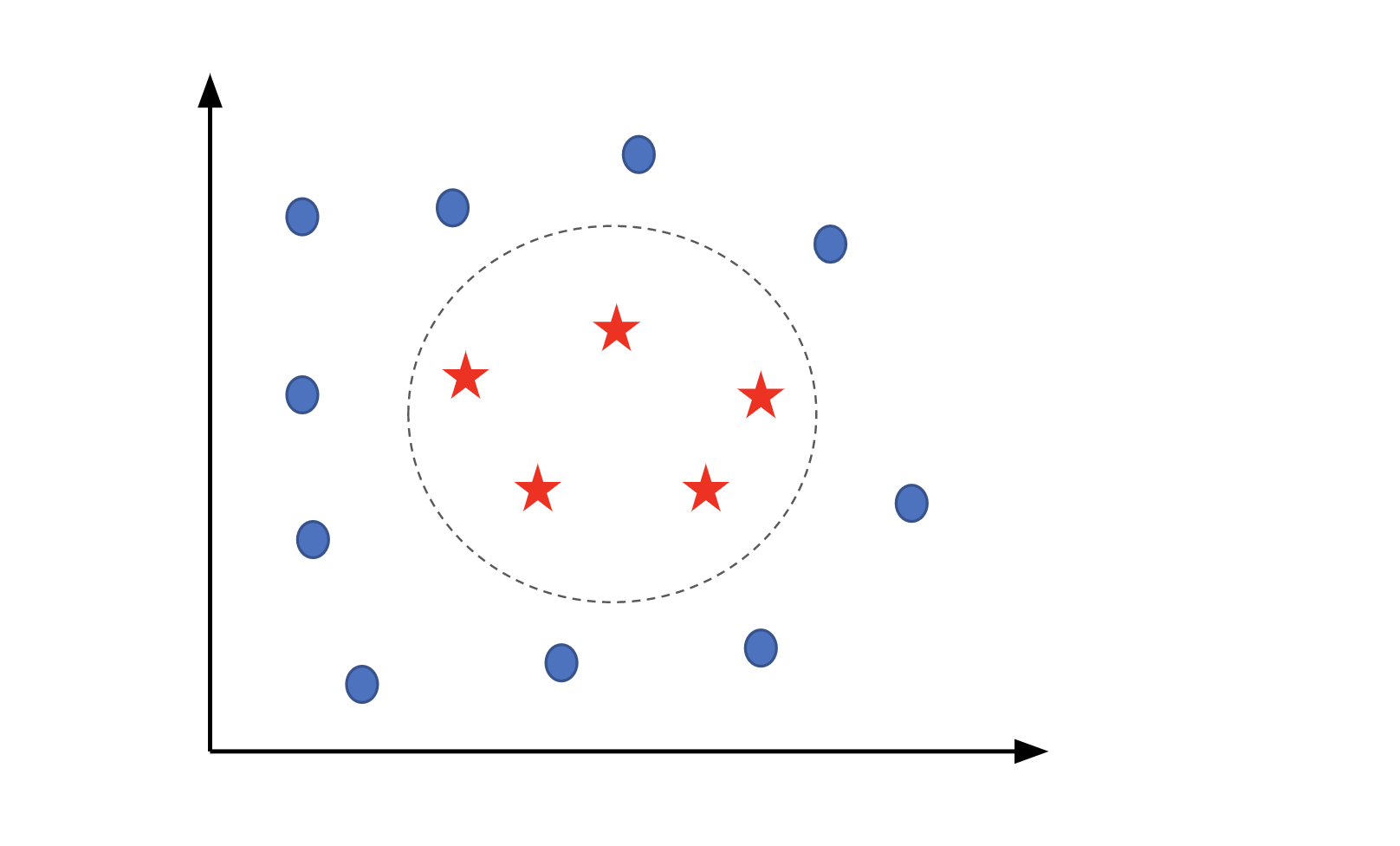
Le cas présenté ci-dessus montre des données linéairement séparables où une simple droite (puisque nous avons deux dimensions) permet de résoudre ce problème de classification. Ceci n’est pas toujours le cas (voir figure ci-dessous). Afin de remédier au problème de l’absence de séparateur linéaire, l’astuce du noyau permet de reconsidérer le problème dans un espace de dimension supérieure où on peut trouver une séparation linéaire. Par exemple, le cas de la figure ci-dessous peut être résolu par l’utilisation d’un noyau polynomial.

Les méthodes ensemblistes

Les méthodes ensemblistes permettent de combiner plusieurs classifieurs afin d’améliorer les résultats. On peut distinguer deux sous-familles:

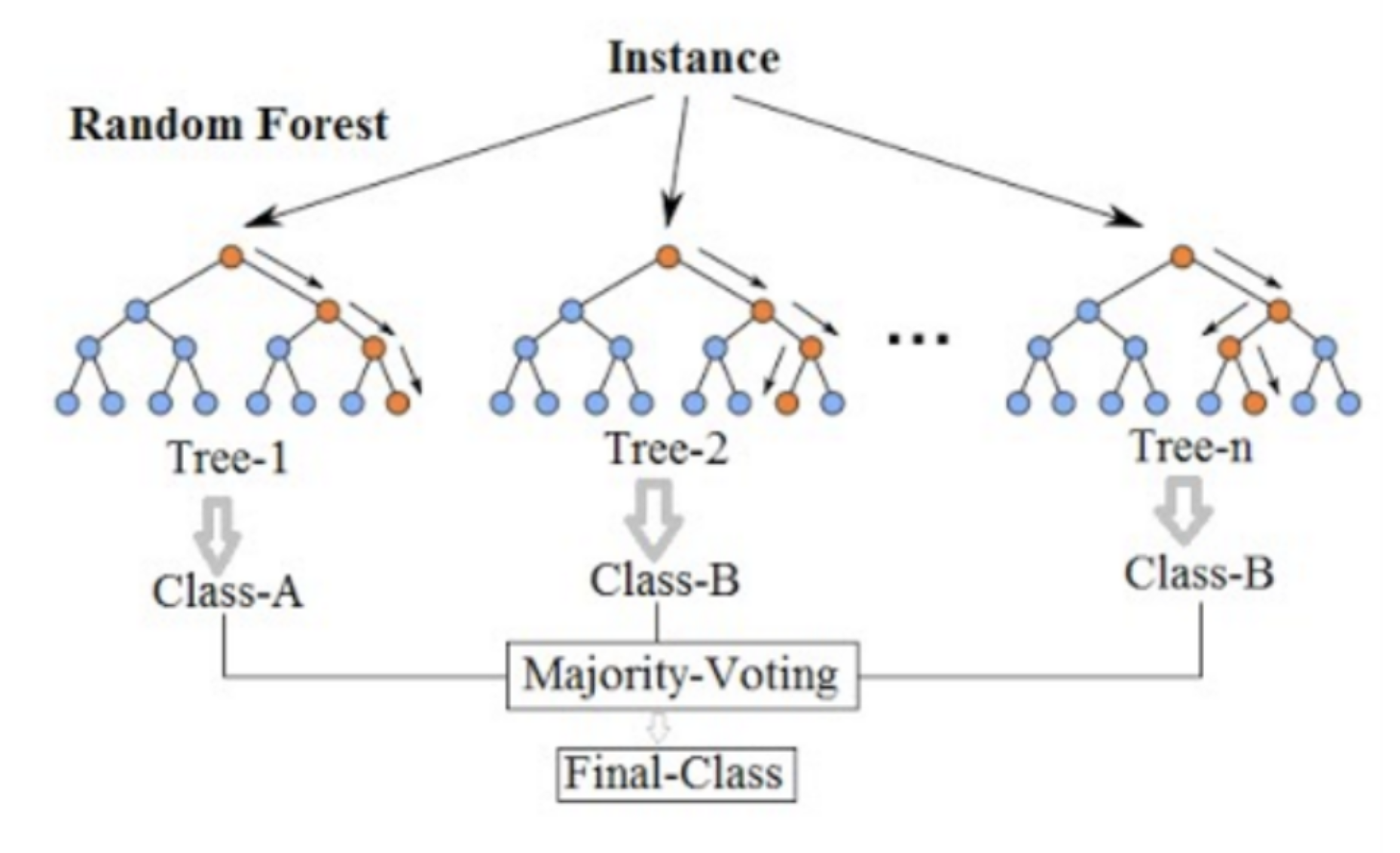
4.1. Le bagging : qui permet d’entraîner plusieurs modèles (classifieurs) en parallèle pour ensuite les regrouper afin de prendre une décision. L’algorithme de bagging le plus connu est le Random Forest dont le principe est d’apprendre plusieurs arbres de manière indépendante sur des échantillons (avec replacement) des données d’apprentissage. La prédiction finale sera agrégée par un vote majoritaire (ou une moyenne des probabilités) issu des prédictions des différents arbres appris.

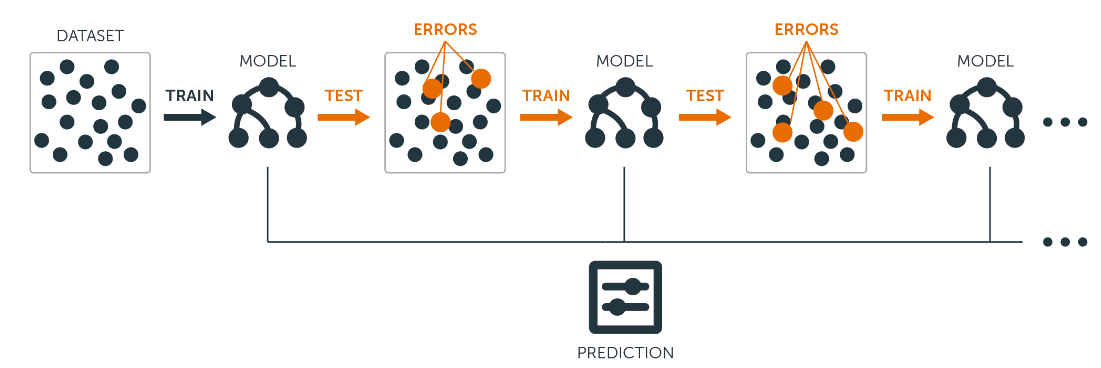
4.2. Le boosting : qui consiste aussi à combiner des classifieurs mais de manière séquentielle (e.g. Ada Boost). L’idée est que le classifieur numéro N se concentre sur les items mal classés par le classifieur numéro N-1. En effet chaque classifieur est entraîné sur un jeu de données pondéré qui accorde plus d’importance aux observations qui ont été mal classées par le classifieur précédent. La prédiction finale est aussi une combinaison pondérée des prédictions de tout les classifieurs appris en fonction de leur performance. Même si on peut théoriquement choisir n’importe quel type de classifieurs, les arbres de décision représentent le type le plus souvent utilisé.

Source de l’image

Les réseaux de neurones

Les réseaux de neurones ont reçu beaucoup d’interêt ces dernières années poussées par les nouvelles puissances de calculs à notre disposition et les résultats qu’ils obtiennent sur les benchmarks de référence dans des domaines très variés. Ici, je vais présenter un des premiers réseaux de neurones utilisé en apprentissage artificiel : Le Multi-Layer Perceptron (MLP).

Comme son nom l’indique, ce modèle est composé de plusieurs perceptrons organisés sous forme de couches. Chaque perceptron reçoit en entrée un certain nombre de valeurs à travers ses connexions entrantes et associe un poids à chacune de ces connexions. Le perceptron effectue une somme pondérée des valeurs en entrée à laquelle il applique une fonction d’activation. Le but de la fonction d’activation est de rajouter de la non-linéarité au modèle lui permettant d’apprendre des comportements plus complexes. La fonction sigmoïde citée plus haut est un excellent exemple de fonction d’activation permettant de rajouter cette non-linéarité.

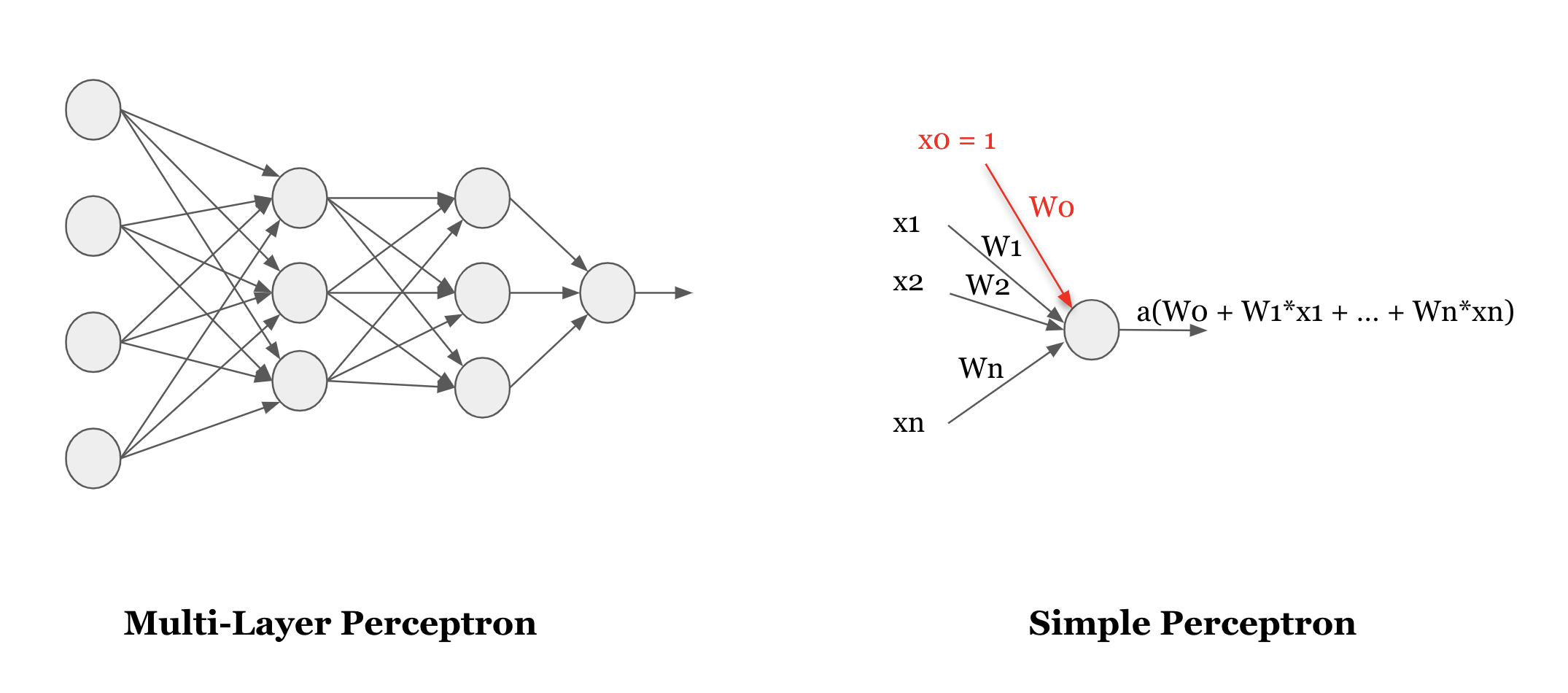
Apprendre un MLP consiste donc à trouver les poids associés à toutes les connexions du réseau. Heureusement pour nous, il existe un algorithme permettant de les trouver en se basant sur les données d’apprentissage, il s’agit de la backpropagation. Très brièvement, l’idée est de partir de valeurs initiales (qui peuvent etre aléatoire) pour ces poids, de comparer les résultats obtenus à la sortie du réseau avec les annotations réelles, et d’ajuster les poids de chaque couche en fonction des ‘erreurs’ obtenues (en partant de la dernière couche et en propageant ces ajustements jusqu’à la première).

Si vous voulez tester les capacités d’apprentissage des réseaux de neurones sur différents types de données, je vous conseille vivement le playground de tensorflow. L’outil est accessible en ligne (pas besoin d’installer quelque chose sur votre ordinateur) et reste très intuitif à l’utilisation. Vous pourrez alors jouer sur le nombre de couches, le nombre de neurones, la fonction d’activation utilisée, lancer des cycles d’apprentissage et voir le comportement du réseau.

Conclusion

Dans cet article, j’ai essayé de présenter l’intuition derrière chaque famille de modèles de Machine Learning supervisé. La liste n’est bien évidemment pas exhaustive et il reste une batterie d’autres modèles que je n’ai pas abordés ici mais je pense avoir couvert les familles les plus connues et les plus utilisées aujourd’hui. J’ai fait en sorte de présenter un modèle par famille (souvent le plus simple à expliquer). Sachez que beaucoup d’améliorations ont été apportées à ces modèles. J’encourage donc ceux qui veulent approfondir leur compréhension des modèles de Machine Learning supervisé à aller plus loin.

Pour aller plus loin

• Le fameux cours d’Andrew Ng sur le Machine Learning
• Le livre de Yoshua Bengio sur le Deep Learning
• Un cours d’OpenClassrooms sur les modèles prédictifs linéaires
• Un cours d’OpenClassrooms sur les modèles prédictifs non-linéaires
• Un cours d’OpenClassrooms sur les modèles ensemblistes
• Un article plus détaillé sur les algorithmes de boosting